今天要來探討「偏度(skewness)與眾數(mode)、中位數(median)、平均數(mean)之關係」,偏度又分成左偏與右偏。先聲明,我不用任何公式去證明他們的關係(因為我也證不出來XD),而是只用概念去分析他們的關係,再來這一篇是很適合給初學者看的一篇文章(因為我自己也是初學者XD,無法用高深的手法去探討)。
首先我們來先分析"(圖二)右偏"這個圖,先讓我們來了解一下圖、眾數、中位數與平均數的意涵。
分析完後,其實只要能真正讀懂圖想要表達的意涵,答案就呼之欲出了!因此,你只要知道圖長怎樣再加上中位數在哪裡,就有能力去判斷出三者間的關係。在此,在更清楚的分析一次:
---
ps. 大家好~我是筆者宗宗,接下來我會陸陸續續將我在大學時期的所見所聞寫成文章,並收錄於我自己的部落格(宗宗大學)。想看更多文章者,歡迎來我的部落格或粉專觀看,喜歡我的文章者歡迎按讚、追蹤、留言與分享,讓我知道 :)。
https://www.facebook.com/ttuniversity2
https://ttuniversity.blogspot.com
---
參考資料:
 |
| (圖一)左偏:平均數<中位數<眾數 |
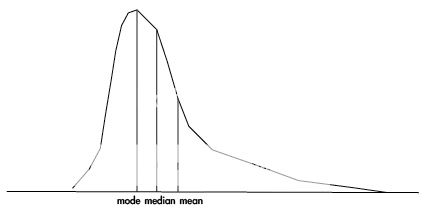 |
| (圖二)右偏:眾數<中位數<平均數 |
- 圖二:此圖x軸表示數值,y軸表示數量,面積表示數量而非數值大小。圖中可以看到以中位數為切割線,左半邊數據的分布是窄而密集,窄的意涵表示這群數據大部分離中位數的距離較近,可能出現離群值(outlier)機率較小,因此左半邊影響平均數的能力較小;右半邊的數據是廣而分散,廣的意涵表示這群數據大部分離中位數的距離較遠,可能出現離群值機率較大,因此右半邊影響平均數的能力較大。
- 眾數:最多個數的數值(圖中的最高峰)。可以利用眾數與中位數來預測數據分布的趨勢(窄而密集或廣而分散)。
- 中位數:整個樣本中,中間那一個數值。也就是說有一半的樣本是比中位數大;另一半的樣本比中位數小,並且中位數那一條直線會將圖的面積平分,意旨左半邊面積=右半邊面積。
- 平均數:BJ4。
分析完後,其實只要能真正讀懂圖想要表達的意涵,答案就呼之欲出了!因此,你只要知道圖長怎樣再加上中位數在哪裡,就有能力去判斷出三者間的關係。在此,在更清楚的分析一次:
- 我已經知道圖長怎樣且知道中位數在哪裡,要如何得出三者間的關係?眾數是最簡單的,因為只要找到圖的最高峰即是,再來看以中位數為分割線左右兩邊數據的分布情形(為什麼要選中位數為切割線?理由就是為了使左右兩邊的數目相同,如果數目不同,很難去比較左右兩邊離切割線的平均距離大小。)如果左邊是窄而密集,右邊是廣而分散,那麼右邊離中位數的平均距離會大於左邊的平均,因此平均數會比中位數還要偏右;如果相反,則反之。
- 已知圖與中位數,但如果不要靠圖,是否能得出三者間的關係?可以,首先找出眾數位在哪裡,如果眾數在中位數的左邊,可以推斷中位數左側的數據是比較密集的,因為眾數是指最多個數的數值,所以相對起來是比較密集的;而中位數右側的數據是比較分散的,因為右側無眾數,那麼可以推斷右邊離中位數的平均距離會大於左邊的平均,因此平均數會比中位數還要偏右;如果相反,則反之。(這也就是為什麼上面第二點說到,可以利用眾數與中位數來預測數據分布的趨勢,但這樣的預測是有缺陷的,因為說不定左側有眾數,但左側其他數值都只有一個;而右側無眾數,但右側其他數值只是比眾數少一點點的數量,因此這個想法無法準確判斷出數據分布的真實情況。)
所以從這些推論中,可以得到:
ps.這裡的想法全部出自於我自己吸收其他知識加統整得到的,所以多少用字上可能為沒那麼精準與專業,甚至想法上會有謬誤,如果有任何問題請留言給我。
- 平均數很容易受到離群值的影響,因此,平均數會偏向離群值多的一方。
- 眾數與中位數不易受到離群值的影響,因此,當離群值很多時,平均數可能不適合來代表整個數據的值。
ps.這裡的想法全部出自於我自己吸收其他知識加統整得到的,所以多少用字上可能為沒那麼精準與專業,甚至想法上會有謬誤,如果有任何問題請留言給我。
---
ps. 大家好~我是筆者宗宗,接下來我會陸陸續續將我在大學時期的所見所聞寫成文章,並收錄於我自己的部落格(宗宗大學)。想看更多文章者,歡迎來我的部落格或粉專觀看,喜歡我的文章者歡迎按讚、追蹤、留言與分享,讓我知道 :)。
https://www.facebook.com/ttuniversity2
https://ttuniversity.blogspot.com
---
參考資料:
- 維基百科。偏度[accessed 30 September 2016]
- Yahoo知識+。請問有關統計學左偏,右偏的問題[accessed 30 September 2016]
- 批踢踢實業坊。[問題]偏離問題[accessed 30 September 2016]
- 批踢踢實業坊。[機統] 高峰左偏右偏時的中位數 眾數 平均數順序[accessed 30 September 2016]
- 國立成功大學 統計學系。請問老師一個笨問題!![accessed 30 September 2016]
留言
張貼留言